Celestial Navigation

This introduction to celestial navigation is provided as a guide to locate geocaches in the "Celestial Navigation"-series (#1, #2) and "Interstellar Message in a Bottle". Some of the concepts in the description are simplified to make the guide as condensed as possible.

Astronav

Although celestial objects (the sun, the moon, planets, stars, etc) are at a wide range of distances from us, to locate them in space, we only need to know their direction. The easiest way to do this is to assume that all objects in space are at the same distance, on the inside of an imaginary celestial sphere. A sphere is a three-dimensional object, but its surface is two-dimensional. So, if we imagine that all celestial objects are on the inside surface of a sphere, we only need two measurements to locate an objects position - a latitude and longitude. This is similar to how we measure locations on the Earth's surface.

Coordinates on Earth are measured in latitude, from 0° at the equator to 90° north and south at the poles, and longitude, running from pole to pole and measured at the Greenwich meridian to 180° east and west.

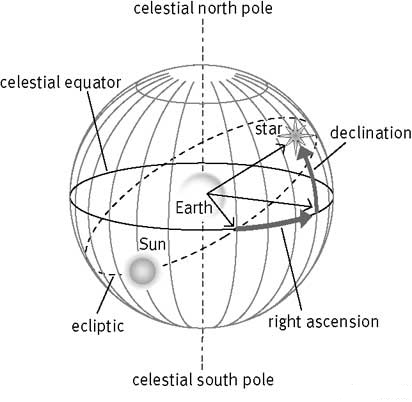
To make the celestial coordinate system work, there must be a line of zero latitude and zero longitude (like the Earth’s equator and Greenwich Meridian). In celestial navigation, this point is called the vernal equinox which is the Spring time intersection of the celestial equator (the Earth’s equator projected outwards on the celestial sphere) and the ecliptic plane (the path the Earth takes around the Sun), a k a the summer solstice (if you are in the Northern Hemisphere). Positions of celestial objects are described by their Right Ascension (the angle eastward from the vernal equinox) and Declination (the angle above or below the celestial equator). Right ascension is measured in hours, minutes and seconds rather than degrees (as we do with the Earth's longitude). One complete circle is 24 hours rather than 360 degrees. Declination is measured in the same way we measure the Earth's latitude and ranges between -90 and +90 degrees measured from the celestial equator.

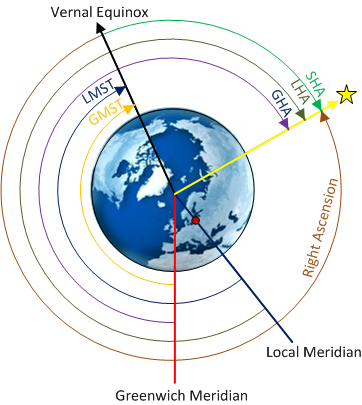Hour AngleGiven the Right Ascension (RA), we can calculate the hour angle which is the angular distance on the celestial sphere measured westward along the celestial equator from the meridian to the position of the observed object on the celestial sphere. There are different types of hour angles; the Greenwich Hour Angle (GHA) which is measured from the prime meridian, the Local Hour Angle (LHA) measured from the local meridian and the Sidereal Hour Angle (SHA) measured from the vernal equinox. The SHA for navigational stars is listed in the Nautical Almanac along with its declination.

Due to the Earth’s rotation, the first step in celestial navigation is to determine the position of the vernal equinox given the time of observation. For celestial navigation, the star constellation Aries is used as a proxy for the vernal equinox so the observer must calculate the GHA for Aries (a k a Greenwich Mean Sidereal Time (GMST)) either through an established formula or through linear interpolation/approximation based on the Nautical Almanac which lists the GHA for Aries in hourly intervals.

To calculate the GHA for Aries, you must first calculate the Julian Day, which is the number of elapsed days (and fractions of a day) since beginning of the Julian Period (12 am, 1 January, 4713 BC) which is a common reference epoch in celestial navigation. The Julian Day for yyyy-mm-dd HH:MM:SS can be calculated with the following formula:

JD = (367 * yyyy - floor(7*(yyyy + floor((mm+9)/12))/4) - floor(3*(floor((yyyy+(mm-9)/7)/100)+1)/4) + floor(275*mm/9) + dd + 1721028.5) + (HH+MM/60+SS/3600) / 24

The term “floor” should be interpreted as rounding down to the nearest integer, e.g. floor(7.98) is 7.

Next, we calculate a factor (T) referred to as Julian Centuries which is a unit of elapsed time since 1 January, 2000, 12 am. The formula is:

T = (JD - 2451545 ) / 36525

Now we can calculate the GHA for Aries at the time of our observation with the following formula:

GHA Aries = (280.46061837 + 360.98564736629 * (JD-2451545) + 0.000387933*T*T - T*T*T/38710000) % 360

The percent sign is a modulus operator. I will not go into details regarding the formula and suffice to say that the formula calculates the angular “movement” of Aries along the celestial sphere since the established epoch (J2000, i.e. 1 January 2000, 12 am) and the modulus of 360 brings the value to an angle in degrees.

Given the value of GHA for Aries and the SHA for a star (or any other celestial object), we can calculate the GHA for the star with this formula:

GHA Star = GHA Aries + SHA Star

By adding the longitude of the observer, we get the LHA for the star:

LHA Star = GHA Star + Longitude

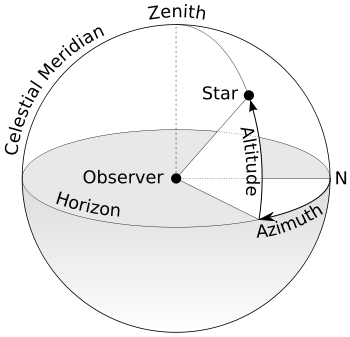
We now have all data required to calculate the Altitude (the angle in degrees above or below the observer’s horizon) of the star through some spherical trigonometry:

Altitude = ARCSIN(SIN(Latitude) x SIN(Declination) + COS(Latitude) x COS(Declination) x COS(LHA Star))

Finally, we can also calculate the Azimuth (the angle in degrees eastward from the observers North along the horizontal plane) of the star with the following formula:

Azimuth = ARCCOS((SIN(Declination) - SIN(Latitude) x SIN(Altitude)) / (COS(Latitude) x COS(Altitude)))

If the LHA is less than 180° then deduct the calculated value above from 360 to get the Azimuth, else you already have the azimuth from the formula above.

That concludes this brief theoretical background and collection of formulas in celestial navigation. The next section describes how these formulas can be put to use to identify an observer’s location on Earth given observations of celestial objects and the time of these observations.

Sight Reduction

This section describes, step-by-step, how to obtain an observer’s location using Sight Reduction. There are multiple alternative methods to get the same result but the benefit of sight reduction is that it does not require programming or in-depth understanding of spherical trigonometry.

Sight Reduction Step-by-step:

  1. Pick a location somewhere near the cache. As long as you are within a couple of kilometers of the actual location, you will be fine. This is your assumed position (AP).
  2. Calculate the GHA for Aries using the formulas above for the three observations.
  3. Calculate the LHA for each star at the time of the observations. Use the longitude of your assumed position. The SHA for each star is available in the Nautical Almanac.
  4. Calculate the altitude (Hc) and azimuth (Zn) of each star. Make sure that you do the calculations in degree mode.
  5. Take the observed altitudes (Ho) of each star and subtract Hc. The difference between Ho and Hc is how far your line of position lies towards the star (negative values means you line of position lies away from the star). One minute of difference is a nautical mile (1852 meters) and consequently one second is around 30 meters. Since the observations are provided with high precision, you should be able to determine each line of position with good accuracy.
  6. Create a grid similar to the picture below in a suitable measurement scale. Observe that distances of longitude depends on your position whereas one minute of latitude is always a nautical mile. Draw a circle and in the center put you assumed position. Then draw lines for each star through AP with the angle of your calculated azimuth (the dotted lines). Based on your calculated differences (Ho-Hc), mark the distances towards or away from the stars from your AP (the dashed lines). For each line at your mark, draw your lines of position (LOP) for each star as perpendicular lines (the solid lines with 90° angle). Where the three LOP lines intersect is the observer’s position (where the cache is located).

If you do not get sufficient precision to pinpoint the coordinates of the cache, you can do another iteration of the steps above and set the AP to coordinates you get from the previous iteration. This way you should get smaller differences between Hc and Ho and it will be easier to draw the LOPs to pinpoint the coordinates of the cache.

To help you draw your own lines of position, you can use this LOP chart and apply a suitable scale. If you are not inclined to drawing, you can obviously achieve the same result by iterating programatically or in Excel so that you adjust your AP to minimize the least squared error of Ho-Hc.